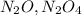Answer : The correct option is, (5)
Explanation :
For 1st experiment :
First we have to calculate the moles of
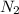 .
.
Molar mass of
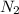 = 28 g/mole
= 28 g/mole

Now we have to calculate the moles of
 .
.
Molar mass of
 = 32 g/mole
= 32 g/mole
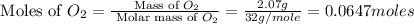
Now we have to calculate the ratio of
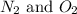 .
.
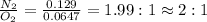
Thus, the molecular formula of the nitrogen oxide will be,
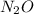 .
.
For 2nd experiment :
First we have to calculate the moles of
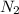 .
.
Molar mass of
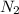 = 28 g/mole
= 28 g/mole
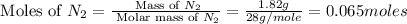
Now we have to calculate the moles of
 .
.
Molar mass of
 = 32 g/mole
= 32 g/mole
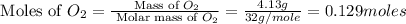
Now we have to calculate the ratio of
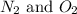 .
.

To make a whole number, we are multiplying the ratio by 2, we get the ratio 1 : 2.
Thus, the molecular formula of the nitrogen oxide will be,
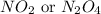 .
.
Hence, the correct option is, (5)