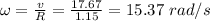Answer:
The angular velocity is 15.37 rad/s
Solution:
As per the question:
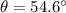
Horizontal distance, x = 30.1 m
Distance of the ball from the rotation axis is its radius, R = 1.15 m
Now,
To calculate the angular velocity:
Linear velocity, v =
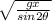
v =
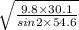
v =
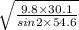
v =
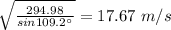
Now,
The angular velocity can be calculated as:
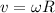
Thus