Question

Express the van der Waals equation of state as a virial expansion in powers of 1/Vm and obtain expressions for B and C in terms of the parameters a and b. The expansion you will need is (1 − x)−1 = 1 + x + x2 + … . Measurements on argon gave B = −21.7 cm3 mol−1 and C = 1200 cm6 mol−2 for the virial coefficients at 273 K. What are the values of a and b in the corresponding van der Waals equation of state?

Answer 1

`PV_(m) = RT[1 + (b-(a)/(RT))(1)/(V_(m) ) + (b^(2) )/(V^(2) _(m) ) + ...]`

B = b -a/RT

C = b^2

a = 1.263 atm*L^2/mol^2

b = 0.03464 L/mol

Step-by-step explanation:

In the given question, we need to express the van der Waals equation of state as a virial expansion in powers of 1/Vm and obtain expressions for B and C in terms of the parameters a and b. Therefore:

Using the van deer Waals equation of state:

`P = (RT)/(V_(m)-b ) - (a)/(V_(m) ^(2) )`

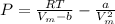
With further simplification, we have:

`P = RT[(1)/(V_(m)-b ) - (a)/(RTV_(m) ^(2) )]`

Then, we have:

`P = (RT)/(V_(m) ) [(1)/(1-(b)/(V_(m) ) ) - (a)/(RTV_(m) )]`

Therefore,

`PV_(m) = RT[(1-(b)/(V_(m) )) ^(-1) - (a)/(RTV_(m) )]`

Using the expansion:

`(1-x)^(-1) = 1 + x + x^(2) + ....`

Therefore,

`PV_(m) = RT[1+(b)/(V_(m) )+(b^(2) )/(V_(m) ^(2) ) + ... -(a)/(RTV_(m) )]`

Thus:

`PV_(m) = RT[1 + (b-(a)/(RT))(1)/(V_(m) ) + (b^(2) )/(V^(2) _(m) ) + ...]` equation (1)

Using the virial equation of state:

`P = RT[(1)/(V_(m) )+ (B)/(V_(m) ^(2))+(C)/(V_(m) ^(3) )+ ...]`

Thus:

`PV_(m) = RT[1+ (B)/(V_(m) )+ (C)/(V_(m) ^(2) ) + ...]` equation (2)

Comparing equations (1) and (2), we have:

B = b -a/RT

C = b^2

Using the measurements on argon gave B = −21.7 cm3 mol−1 and C = 1200 cm6 mol−2 for the virial coefficients at 273 K.

`b = √(C) = √(1200) = 34.64[tex]cm^(3)/mol`[/tex] = 0.03464 L/mol

a = (b-B)*RT = (34.64+21.7)*(1L/1000cm^3)*(0.0821)*(273) = 1.263 atm*L^2/mol^2