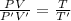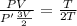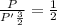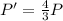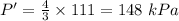Question

A system of ideal gas has an initial pressure of 111 kPa and occupies a volume of 5.00 liters. Doubling the system’s absolute temperature by means of a constant-pressure process would require an amount of work W. Instead, you decide to double the absolute temperature by carrying out two processes in sequence, a constant-pressure process followed by a constant-volume process. In this case, the total work done in the two-process sequence is W/2. Calculate the final pressure of the system.

Answer 1

The final pressure is 148 kPa

Solution:

As per the question:

Initial Pressure of the gas, P = 111 kPa

Initial Volume, V = 5.00 l

Now,

In order to calculate the final pressure of the system:

At constant pressure, the work done is 'W'

If the absolute initial temperature be T

When the absolute temperature is doubled, T' =2T

Total work done in the processes, W =
`(W)/(2)`

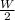
Now,

From the ideal gas eqn:

PV = nRT

PV ∝ T (1)

In constant pressure process, work done is given by:

W =
`P\Delta V` (2)

Thus from eqn (1) and (2):

`(V)/(V')= (T)/(T')`

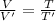
In the first process, temperature is doubled:

`(V)/(V')= (T)/(2T)`

V = 2V'

Thus

`V' = (V)/(2)`

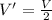
In the process, the change in volume is
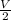`(V)/(2)` given by:

`V_(t) = V + (V)/(2) = (3V)/(2)`

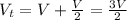
Now,

`(PV)/(P'V') = (T)/(T')`

`(PV)/(P'(3V)/(2)) = (T)/(2T)`

`(P)/(P'(3)/(2)) = (1)/(2)`

`P' = (4)/(3)P`

`P' = (4)/(3)* 111 = 148\ kPa`