Question

A sample of 900 college freshmen were randomly selected for a national survey. Among the survey participants, 372 students were pursuing liberal arts degrees. The sample proportion is 0.413.What is the margin of error for a 99% confidence interval for this sample? What is the lower endpoint for the 99% confidence interval?

Answer 1

a)
`ME=2.58 \sqrt{(0.413(1-0.413))/(900)}=0.0423`

b)
`0.413 - 2.58 \sqrt{(0.413(1-0.413))/(900)}=0.371`

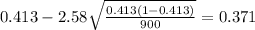
Explanation:

1) Data given and notation

n=900 represent the random sample taken

X=372 represent the students were pursuing liberal arts degrees

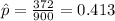`\hat p=(372)/(900)=0.413` estimated proportion of students were pursuing liberal arts degrees

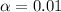`\alpha=0.01` represent the significance level

z would represent the statistic (variable of interest)

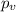`p_v` represent the p value (variable of interest)

p= population proportion of students were pursuing liberal arts degrees

2) Solution to the problem

The confidence interval would be given by this formula

`\hat p \pm z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

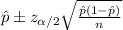
For the 99% confidence interval the value of
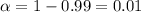`\alpha=1-0.99=0.01` and
`\alpha/2=0.005`, with that value we can find the quantile required for the interval in the normal standard distribution.

`z_(\alpha/2)=2.58`

The margin of error is given by:

`ME=z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

If we replace we have:

`ME=2.58 \sqrt{(0.413(1-0.413))/(900)}=0.0423`

And replacing into the confidence interval formula we got:

`0.413 - 2.58 \sqrt{(0.413(1-0.413))/(900)}=0.371`

`0.413 + 2.58 \sqrt{(0.413(1-0.413))/(900)}=0.455`

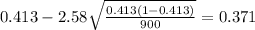
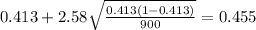
And the 99% confidence interval would be given (0.371;0.455).

We are confident (99%) that about 37.1% to 45.5% of students were pursuing liberal arts degrees.