Answer:
Arithmetic average rate of return = 9.30 %
geometric average annual rate of return = 8.58%
correct option is A 9.30 % and 8.58%
Step-by-step explanation:
given data
beginning share price = $50
time = 3 year
end year 1 prices = $62
end year 2 prices = $58
end year 3 prices = $64
to find out
arithmetic average annual rate of return and the geometric average annual rate of return
solution
we get here return for each period that is express as
Period 1 =
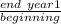 ...........1
...........1
Period 1 =
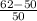
Period 1 = 24%
and
Period 2 =

Period 2 = Period 1 =
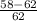
Period 2 = -6.45%
and
Period 3 =
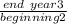
Period 3 =
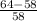
Period 3 = 10.34%
so
here Arithmetic average rate of return will be
Arithmetic average rate of return = (24% + -6.45% + 10.34%) ÷ 3
Arithmetic average rate of return = 9.30%
and
geometric average annual rate of return will be here as
geometric average annual rate of return =
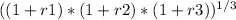 - 1 ................2
- 1 ................2
geometric average annual rate of return =
 - 1
- 1
geometric average annual rate of return = 8.58%