Answer:
(a)
![[Y_(p) ]_(max) = (2f)/(1+f)](https://img.qammunity.org/2020/formulas/physics/college/o2yh5k8e4xtmnaz5rsjo065idnxym1rtfw.png)
(b)
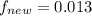 ;
;
![[Y_(p) ]_(max)](https://img.qammunity.org/2020/formulas/physics/college/setw8f4xcb66j3ckpunevwlnshra8pi8mz.png) = 0.026
= 0.026
Step-by-step explanation:
Since the neutron-to-proton ratio at the time of nucleosynthesis is given:
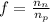
Therefore:
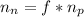
Then, to determine the maximum ⁴He fraction if all the available
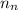 neutrons bind to all the protons. Since, there are 2 protons and 2 neutrons in a ⁴He nucleus, it shows that there would be
neutrons bind to all the protons. Since, there are 2 protons and 2 neutrons in a ⁴He nucleus, it shows that there would be
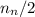 nuclei of ⁴He.
nuclei of ⁴He.
In addition, a ⁴He nucleus has a mass of
 , where
, where
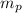 is the mass of one proton. Thus,
is the mass of one proton. Thus,
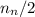 nuclei of such nuclei will have a mass of
nuclei of such nuclei will have a mass of
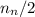 *
*
 .
.
Assuming that
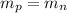 , there would be a total of
, there would be a total of
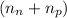 protons and neutrons with a total mass of
protons and neutrons with a total mass of
 .
.
Thus:
![[Y_(p) ]_(max) = (2f)/(1+f)](https://img.qammunity.org/2020/formulas/physics/college/o2yh5k8e4xtmnaz5rsjo065idnxym1rtfw.png)
(b) Given:
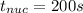 ; τ
; τ
 = 3*60s = 180 s
= 3*60s = 180 s
![f_(new) = (n_(nf) )/(n_(pf) ) = (exp (-200/180))/(5 +[1- exp(-200/180)]) =(0.077)/(5.923) = 0.013](https://img.qammunity.org/2020/formulas/physics/college/noaw9ihfoh3ywo64trygym2y64wnii1g7s.png)
![[Y_(p) ]_(max) = (2f)/(1+f)](https://img.qammunity.org/2020/formulas/physics/college/o2yh5k8e4xtmnaz5rsjo065idnxym1rtfw.png) = (2*0.013)/(1+0.013) = 0.026
= (2*0.013)/(1+0.013) = 0.026