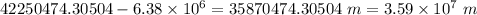Question

Find the radius R of the orbit of a geosynchronous satellite that circles the Earth. (Note that R is measured from the center of the Earth, not the surface of the Earth.) Use the following values if needed in this problem: The universal gravitational constant G is 6.67×10−11Nm2/kg2. The mass of the earth is 5.98×1024kg. The radius of the earth is 6.38×106m. Express your answer numerically in meters to three significant figures.

Answer 1

`3.59* 10^(7)\ m`

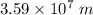
Step-by-step explanation:

r = Distance from the surface

T = Time period = 24 h

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

m = Mass of the Earth = 5.98 × 10²⁴ kg

From Kepler's law which balances centripetal force and the force of gravity we have relation

`T^2=(4\pi^2r^3)/(GM)\\\Rightarrow r=(T^2GM)/(4\pi^2)\\\Rightarrow r=\left(((24* 3600)^2* 6.67* 10^(-11)* 5.98* 10^(24))/(4\pi^2)\right)^{(1)/(3)}\\\Rightarrow r=42250474.30504\ m`

Distance from the center of the Earth would be

`42250474.30504-6.38* 10^6=35870474.30504\ m=3.59* 10^(7)\ m`