Answer:
B. Yes, the proportion of girls is significantly different from 0.5
Explanation:
Given that a clinical trial tests a method designed to increase the probability of conceiving a girl. In the study 340 babies wereborn, and 306 of them were girls.
Sample proportion =
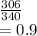
Std error of p =
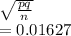
For sample size large, we find that t distribution almost coincides with z distribution
Hence 99% critical value = 2.58
Margin of error = 2.58*std error = 0.0420
Confidence interval =
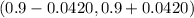
=
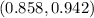
0.858<p<0.942
Yes, this method is effective becuse lower bound itself is 0.858 i.e. there is 85.8%chance for getting girls in birth
B. Yes, the proportion of girls is significantly different from 0.5