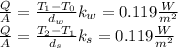Question

A carpenter builds an exterior house wall with a layer of wood 3.0 cm thick on the outside and a layer of Styrofoam insulation 2.4 cm thick on the inside wall surface. The wood has k=0.080W/(m?K), and the Styrofoam has k= 0.010 W/(m?K). The interior surface temperature is 20.0 ?C , and the exterior surface temperature is -13.0 ?C

A.) What is the temperature at the plane where the wood meets the Styrofoam? _______ Celsius
B.) What is the rate of heat flow per square meter through this wall? ______W/m^2

Answer 1

A. T=15.54 °C

B. Q/A= 0.119 W/m2

Step-by-step explanation:

To solve this problem we need to use the Fourier's law for thermal conduction:

`Q= kA(dT)/(dx)`

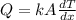
Here, the rate of flow per square meter must be the same through the complete wall. Therefore, we can use it to find the temperature at the plane where the wood meets the Styrofoam as follows:

`(Q)/(A) =(T_1-T_0)/(d_w)k_w=(T_2-T_1)/(d_s)k_s\\T_1((k_w)/(d_w)+(k_s)/(d_s))=T_2(k_s)/(d_s)+T_0(k_w)/(d_w)\\T_1=(T_2(k_s)/(d_s)+T_0(k_w)/(d_w))/((k_w)/(d_w)+(k_s)/(d_s))\\T_1= 15.54 \°C`

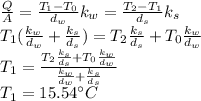
Then, to find the rate of heat flow per square meter, we have:

`(Q)/(A)=(T_1-T_0)/(d_w)k_w=0.119 (W)/(m^2)\\(Q)/(A)=(T_2-T_1)/(d_s)k_s= 0.119 (W)/(m^2)`

`T_0: Temperature \ in \ the \ house\\T_1: Temperature \ at \ the \ plane \ between \ wood \ and \ styrofoam\\T_2: Temperature \ outside\\k_w: k \ for \ wood\\d_w: wood \ thickness\\k_s: k \ for \ styrofoam\\d_s: styrofoam \ thickness`