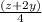Question

Simplify the following rational expression and express in expanded form.

Answer 1

The solution for given expression is
`((z + 2y))/(4)`

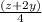
Solution:

Given that rational expression is:

`(z^(2)+4 z y+4 y^(2))/(4 z+8 y)`

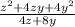
Taking "4" as common term from denominator,

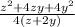`(z^(2)+4 z y+4 y^(2))/(4(z + 2y))` ------- eqn 1

Let us use a algebraic identity which is as follows:

`(a + b)^2 = a^2 + 2ab + b^2`

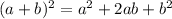
So,
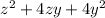`z^(2)+4 z y+4 y^(2)` can be expressed as:

`z^(2)+4 z y+4 y^(2) = (z + 2y)^2`

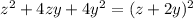
Substitute the above equation in eqn 1,

`((z + 2y)^2)/(4(z + 2y))`

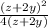
Cancelling (z + 2y) in numerator and denominator

`\rightarrow ((z + 2y))/(4)`

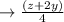
Thus the solution for given expression is
`((z + 2y))/(4)`