Question

During a period of 11 years 653 of the people selected for grand jury duty were​ sampled, and 72​% of them were immigrants. Use the sample data to construct a​ 99% confidence interval estimate of the proportion of grand jury members who were immigrants. Given that among the people eligible for jury​ duty, 68.7​% of them were​ immigrants, does it appear that the jury selection process was somehow biased against​ immigrants?

Answer 1

99% confidence interval estimate of the proportion of grand jury members who were immigrants would be 0.72±0.045, that is (0.675, 0.765) or (67.5%, 76.5%)

Since 68.7​% falls in the confidence interval, there is no significant evidence that the jury selection process was somehow biased against​ immigrants

Explanation:

Confidence Interval can be calculated using p±ME where

• p is the sample proportion of the people selected for grand jury duty members who were​ immigrants. (72% or 0.72)

• ME is the margin of error from the mean

and margin of error (ME) can be found using the formula

ME=
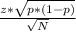`(z*√(p*(1-p)))/(√(N) )` where

• z is the corresponding statistic in 99% confidence level (2.58)

• p is the sample proportion (72% or 0.72)

• N is the sample size (653)

Then ME=
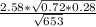`(2.58*√(0.72*0.28))/(√(653) )` ≈ 0.045

99% confidence interval would be 0.72±0.045, that is (0.675, 0.765)