Question

To obtain an estimate of the proportion of "full time" university students who have a part time job in excess of 30 hours per week, the student union decides to interview a random sample of full time students. They want the length of their 90% confidence interval to be no greater than 0.2 with standard deviation is known to be 3 hours. What size of the sample, n should be taken? Round up your answer to the nearest whole number.

Answer 1

2,436 students

Explanation:

At a 90% confidence level, the z-score is 1.645 and the confidence interval is given by:

`x\pm z(s)/(\sqrt n)`

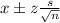
Where s is the standard deviation, and n is the sample size.

If they want the length of their confidence interval to be no greater than 0.2, it must be no further than 0.1 from the mean 'X':

`0.1>1.645(3)/(\sqrt n)\\\sqrt n>1.645*30\\n>2,435.42`

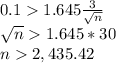
Rounding up to the next whole number, the sample size should be 2,436 students.