Answer:
$7,500
Explanation:
Integrating the daily marginal cost per unit function (C'(x)) at the interval from 0 to 300 units gives us the total variable cost incurred by Ditton in producing he first 300 units.
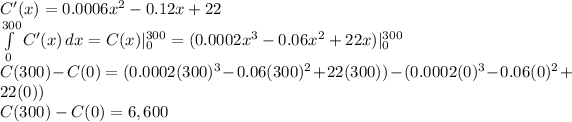
The variable cost incurred is $6,600
The total cost is given by sum of the variable cost and the fixed cost:
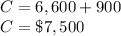
The total cost incurred by Ditton in producing the first 300 units of these toaster ovens per day is $7,500.