Question

The tub of a washer goes into its spin-dry cycle, starting from rest and reaching an angular speed of 7.0 rev/s in 9.0 s. At this point, the person doing the laundry opens the lid, and a safety switch turns off the washer. The tub slows to rest in 11.0 s. Through how many revolutions does the tub turn during this 20 s interval

Answer 1

69.970 rev

Step-by-step explanation:

Case 1: until the washer reaches its top spin

Initial angular speed ωi = 0 rev /s

Final angular speed ωf = 7 rev /s

Time t = 9 s

The angular acceleration is

ωf - ωi = α t

α = 7 - 0 / 9

`= 0.77rev/s^2`

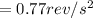
The angular displacement

`θ_1 = \omega_i t + (1/2) \alpha t^2`

`=0 + (1/2)(0.77)(9)^2`

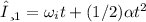
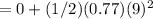
= 31.185 rev

Case II: the washer coming to rest from top spin

Initial angular speed ωi = 7 rev /s

Final angular speed ωf = 0 rev /s

Time t = 11 s

The angular acceleration is

ωf - ωi = α t

α = 0 - 7 / 11

= - 0.63 rev/s^2

The angular displacement

`\theta_2 = \omega_i t + (1/2)\alpha t^2`

`=7(11) + (1/2) (-0.63)(11)^2`

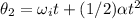
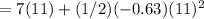
=38.885 rev

Total number of revolutions

θ1 + θ2 = 31.185 rev + 38.885 rev

= 69.970 rev