Answer:
74.31353
=74 m
Explanation:
given that three locations are marked next to a river. Points B and C are on the same side of the river, and point A is on the other side of the river. To find the distance AB across a river, a distance BC of 241 meters is laid off on one side of the river. It is found that the angle at point B is 108.6° and the angle at point C is 14.9°.
we have information about triangle ABC as side BC =241, Angle B = 108.6 and angle C = 14.9 degrees.
Hence this is an obtuse scalene triangle.
Angle ∠A = 56.5° (III angle)
Using sine formula we get
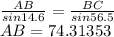
So distance AB is 74 metres.