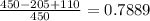Answer:
Explanation:
Given that Of 450 college students, 110 are enrolled in math, 205 are enrolled in English, and 50 are enrolled in both. If a student is selected at random
the probability
(a) The student is enrolled in mathematics=
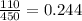
(b) The student is enrolled in English.=

(c) The student is enrolled in both.=
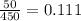
(d) The student is enrolled in mathematics or English.=
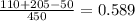
(e) The student is enrolled in English but not in mathematics.
=
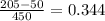
(f) The student is not enrolled in English or is enrolled in mathematics.
=