Answer:
h = 5.45 m
Step-by-step explanation:
Let's perform this exercise in parts, let's look for the speed of the balls when they reach the ground, for this we use the concepts of energy conservation
Initial, at the point where they are released
Em₀ = U = m gh
Fianl on reaching the ground
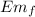 = ½ m v²
= ½ m v²
Em₀ =
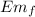
mgh = ½ m v²
v = √ 2gh
We see that the speed of the two balls is the same when they reach the ground, because it does not depend on the mass
v = √ (2 9.8 1)
v = 4,427 m / s
Now let's use the conservation of the amount of movement to find the velocity of the heaviest ball when it bounces on the ground.
Before crash
p₀ = Mv
After it bounces
 = -M v
= -M v
p₀ =

-M v = M

 = -v
= -v
The ball bounces with the same speed, but in the opposite direction
Now let's study the clash of the two balls, suppose it has the same small diameter, the magnitude of the velocity is the same, but the large bullet has an upward direction (positive)
Initial before the crash
p₀ = M v - m v
After the crash
 = m
= m
 + M
+ M

p₀ =

(M-m) v = m
 + M
+ M

As the shock is elastic the kinetic energy is conserved
K₀ = ½ M v² + ½ m v²
K₀ = ½ (M + m) v²
 = ½ m
= ½ m
 ² + ½ M
² + ½ M
 ²
²
K₀ =

(M + m) v² = m
 ² + v
² + v
 ²
²
Let's write and solve our system of equations
(M-m) v = m v1f + M v2f
(M + m) v² = m
 ² +M
² +M
 ²
²
Let's replace
0.4 4.427 = 0.1 v1f +0.5 v2f
0.6 4.427² = 0.1
 ² + 0.5
² + 0.5
 ²
²
1.77 = 0.1 v1f +0.5 v2f
11.76 = 0.1
 ² + 0.5
² + 0.5
 ²
²
 = (1.77 - 0.1
= (1.77 - 0.1
 ) / 0.5
) / 0.5
I substitute in the other equation
11.76 = 0.1
 ² + (1.77 -0.1
² + (1.77 -0.1
 )² / 0.5
)² / 0.5
11.76= 0.1
 ² + 6.2658 - 0.708
² + 6.2658 - 0.708
 + 0.02
+ 0.02
 ²
²
0.12
 ² - 0.708
² - 0.708
 -5.4942 = 0
-5.4942 = 0
 ² - 5.9
² - 5.9
 - 45. 785 = 0
- 45. 785 = 0
Let's solve the second degree equation
 = [5.9 ±√(5.9 2 + 4 45,785)] / 2 = [5.9 + - 14.76] / 2
= [5.9 ±√(5.9 2 + 4 45,785)] / 2 = [5.9 + - 14.76] / 2
Results
 = 10.3315 m / s
= 10.3315 m / s
 = -4.43 m / s
= -4.43 m / s
The correct result is the positive, since the negative result the lighter ball should follow its trajectory, which is impossible since the heaviest is going up
 = 10. 3315 m / s
= 10. 3315 m / s
With this speed we can use energy to calculate until the lightest ball rises
Initial
Em₀ = K = ½ m
 ²
²
Final
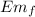 = U = m g h
= U = m g h
Em₀ =
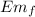
½ m
 ² = m g h
² = m g h
h = ½
 ² / g
² / g
h = ½ 10.3315² / 9.8
h = 5.45 m