Answer:
Given function is:
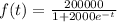
Part A:
When t = 0

=
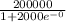
=
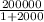
=
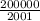
= 99.95 rounding to 100 people.
Part B:
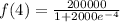
=
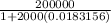
=
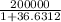
=
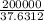
= 5314.73
So, approximately 5,315 people were ill by the end of the 4th week.
Part C:
Let 't' be approaching infinity.
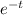 will approach zero, so f(infinity)=
will approach zero, so f(infinity)=
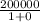
f(infinity)=200000
Hence, the limit is that all of the persons can become ill.