Answer:
x₀ = 1,894 m
Step-by-step explanation:
For this exercise let's use Hooke's law
F = - k Δx = - k (
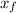 –x₀)
–x₀)
Let's write this equation for the given conditions, the extended length of the spring is the final length (xf = 2.45 m), the sense of force always opposes displacement
With the force applied
F = -k (
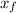 - x₀)
- x₀)
(
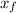 - x₀) = - F / k
- x₀) = - F / k
x₀ =
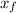 + F / k
+ F / k
x₀ = 2.45 + (-20.0) / 36.0
x₀ = 2.45 - 0.556
x₀ = 1,894 m
This is the so-called natural spring length