Question

a carpenter has been asked to build an open box with a sqaure base. the sides of the box will cost $3 per m^2 and the base will cost $4 per m^2. What are the dimensions of the box of greatest volume that can be constructed for $48

Answer 1

Dimension of box is 2 m x 2 m x 1.33 m

Explanation:

Let a be base side and h be the height.

Volume of box, V = a²h

The sides of the box will cost $3 per m² and the base will cost $4 per m². Cost for making is $48.

That is

4a² + 3 x 4 x a x h = 48

4a² + 12 a x h = 48

a² + 3 ah = 12

`h=(12-a^2)/(3a)`

So volume is

`V=a^2* (12-a^2)/(3a)=4a-(a^3)/(3)`

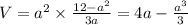
At maximum volume we have derivative is zero,

`dV=4da-3* (a^2)/(3)da\\\\0=4-a^2\\\\a=\pm 2`

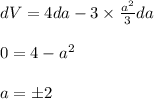
Negative side is not possible, hence side of square base is 2m.

Substituting in a² + 3 ah = 12

2² + 3 x 2 x h = 12

h = 1.33 m

Dimension of box is 2 m x 2 m x 1.33 m