Answer:
a) I = 1,944 10⁻⁴⁶ Kg m²
, b) I = 7,915 10⁻⁵¹ Kg m²
Step-by-step explanation:
a) The moment of inertia of point masses is
I = m r²
The nuclei have a very small size (10-15 m) so we can consider them punctual.
The distance to the center of mass passing through the middle of the two nuclei of equal mass
r = 0.6 10⁻¹⁰ m
The moment of total inertia
I = I₁ + I₂ = 2 I₀
I = 2 2.7 10⁻²⁶ (0.6 10⁻¹⁰)²
I = 1,944 10⁻⁴⁶ Kg m²
The kinetic energy of the rotation is
w = h / 2π
K = ½ I w²
K = ½ 1,944 10⁻⁴⁶ (h / 2π)² = ½ 1.944 10⁻⁴⁶ (6.63 10⁻³⁴ / 2π)²
K = 2.16 10⁻¹¹⁴ J (1eV / 1.6 10⁻¹⁹ J)
K = 2.16 10⁻⁹⁵ eV
B) the moment of inertia of the electron in the orbit, we can calculate it with the parallel axis theorem
I =
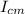 + m R²
+ m R²
I =
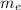 r² +
r² +
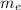 R²
R²
Where R we calculate it by Pythagoras
R² = (0.6 10⁻¹⁰)² + (0.5 10⁻¹⁰) 2
R = √ (0.61 10⁻²⁰)
R = 0.78 10⁻¹⁰ m
I = 9.1 10⁻³¹ (0.5 10⁻¹⁰)² + 9.1 10⁻³¹ (0.78 10⁻¹⁰)²
I = (2,275 +5.54) 10⁻⁵¹
I = 7,915 10⁻⁵¹ Kg m²
The rotation energy of the electron
K = ½ I w²
If the angular velocity is the electrons outside the core, its kinetic energy is much lower by an order 10⁵, but the angular velocity of the electrons is much higher.