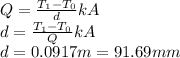Answer:
The Cu plate must be at least 91.69 mm thick
Step-by-step explanation:
To solve this problem we need to use the Fourier's law for thermal conduction:
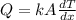
Here, we must solve the equation for d, assuming that the maximum possible temperature of the other side of the plate is 24°C: