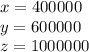Answer:
x=400000\\y=600000\\z=1000000
Explanation:
Given that a trust account manager has $2,000,000 to be invested in three different accounts. The accounts pay 6%, 8%, and 10%, and the goal is to earn $172,000 with the amount invested at 10% equal to the sum of the other two investments.
To accomplish this, assume that x dollars are invested at 8%, y dollars at 10%, and z dollars at 6%.
The equations formed would be
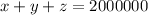
Interest amount =
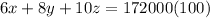
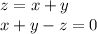
these three can be written in matrix form as
![\left[\begin{array}{ccc}1&1&1\\6&8&10\\1&1&-1\end{array}\right] =\left[\begin{array}{ccc}200000\\17200000\\0\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/gcpxethvhellv6p23vfffi1nqcdwq5tr56.png)
The inverse of the matrix is
![\left[\begin{array}{ccc}9/2&-1/2&-1/2\\-4&1/2&1\\1/2&0&-1/2\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/high-school/rsa9tsczx5glhx0odtk5qj6grza4c3vedd.png)
X = A inverse *B
Using this we get