Question

A $1,000 par value bond was issued five years ago at a 8 percent coupon rate. It currently has 25 years remaining to maturity. Interest rates on similar debt obligations are now 10 percent. Use Appendix B and Appendix D for an approximate answer but calculate your final answer using the formula and financial calculator methods. a. Compute the current price of the bond using an assumption of semiannual payments. (Do not round intermediate calculations and round your answer to 2 decimal places.) b. If Mr. Robinson initially bought the bond at par value, what is his percentage capital gain or loss? (Ignore any interest income received. Do not round intermediate calculations and input the amount as a positive percent rounded to 2 decimal places.) c. Now assume Mrs. Pinson buys the bond at its current market value and holds it to maturity, what will be her percentage capital gain or loss? (Ignore any interest income received. Do not round intermediate calculations and input the amount as a positive percent rounded to 2 decimal places.) d. Why is the percentage gain larger than the percentage loss when the same dollar amounts are involved in parts b and c? The percentage gain is larger than the percentage loss because the investment is larger. The percentage gain is larger than the percentage loss because the investment is smaller.

Answer 1

a: current value of the bond $405.11

b: Robison loss: 59.49%

c Pinson gain: 146.85%

As the investment is smaller the percentage change at maturity is greater than the difference in percentage of the par value.

A percent of the original investmentrepresent 10 dollars while !% of Mrs Pinson represent 4.05 dollars

Step-by-step explanation:

The present value of the bonds is the sum of the present value of the coupon payment and the maturity discounted at market rate:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C: 1,000 x 8% / 2 = 40.00

time: 25 years x 2 payment per year = 50

market rate 0.10

`40 * (1-(1+0.1)^(-50) )/(0.1) = PV\\`

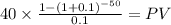
PV $396.5926

`(Maturity)/((1 + rate)^(time) ) = PV`

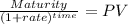
Maturity 1,000.00

time 50.00

rate 0.1

`(1000)/((1 + 0.1)^(50) ) = PV`

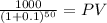
PV 8.52

PV c $396.5926

PV m $8.5186

Total $405.1111

Robinson capital loss:

405.1111/ 1,000 -1 = -59.49%

If purchased today and held to maturity by Mrs Pinson:

1,000 / 405.1111 - 1 = 146.85%