Question

In a study to estimate the proportion of residents in a certain city and its suburbs who favor the construction of a nuclear power​ plant, it is found that 68 of 100 urban residents favor the construction while only 58 of 125 suburban residents are in favor. Is there a significant difference between the proportions of urban and suburban residents who favor construction of the nuclear​ plant? Make use of a​ P-value.

Answer 1

Assuming 0.05 significance level, there is significant difference between the proportions of urban and suburban residents who favor construction of the nuclear​ plant.

Explanation:

Let p(u) be the urban proportion who support nuclear power plant construction

and p(s) be the suburban proportion who support nuclear power plant construction. Then

`H_(0)` : p(u) = p(s)

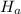`H_(a)` : p(u) ≠ p(s)

The formula for the test statistic is given as:

z=
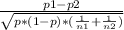`\frac{p1-p2}{\sqrt{{p*(1-p)*((1)/(n1) +(1)/(n2)) }}}` where

• p1 is the sample proportion of urban population who support nuclear power plant construction (
  `(68)/(100)` =0.68)

• p2 is the sample proportion of suburban population who support nuclear power plant construction (
  `(58)/(125)` =0.464)

• p is the pool proportion of p1 and p2 (
  `(68+58)/(100+125)=0.56`)

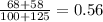• n1 is the sample size of urban population (100)

• n2 is the sample size of suburban population (125)

Then z=
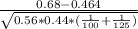`\frac{0.68-0.464}{\sqrt{{0.56*0.44*((1)/(100) +(1)/(125)) }}}` ≈ 3.24

P-value of test statistic is ≈ 0.0012

Since p-value (0.0012 ) < significance level (0.05) we can reject the null hypothesis.