Question

A centrifugal pump rotates at n˙ = 740 rpm. Suppose the pump has some swirl at the inlet (α1 = 10°) and exits at an angle of 35° from radial (α2 = 35°). The inlet radius is r1 = 12.0 cm, at which the blade width b1 = 18.0 cm. The outlet radius is r2 = 24.0 cm, at which the blade width b2 = 16.2 cm. The volume flow rate is 0.573 m3/s. Assuming 100 percent efficiency, calculate the net head produced by this pump in "m" of water column height. Also calculate the required brake horsepower in W. The density of water is taken as rho = 998.0 kg/m3.

Answer 1

Net head = 380cm

bhp = 17.710kW

Step-by-step explanation:

Angular velocity of centrifugal pump:

`w=(2\pi n)/(60)=(2\pi (750))/(60)=78.54(rad)/(s)`

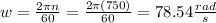
Normal velocity component at outlet of pump:

`V_(2,n)=(V)/(2\pi r_(2)b_(2))=(0.573)/(2\pi (0.24)(0.162))}=2.346(m)/(s)`

Tangential velocity component at exit of the pump:

`V_(2,t)=v_(2,n)tan\alpha _(2)=(2.346)tan(35)=1.643(m)/(s)`

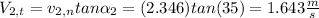
Normal velocity component at inlet of pump:

`V_(1,n)=(V)/(2\pi r_(1) b_(1))=(0.573)/(2\pi (0.12)(0.18))=4.22(m)/(s)`

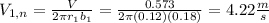
Tangential velocity component at inlet of the pump:

`V_(1,t)=v_(1,n)tan\alpha _(1)=(4.22)tan(0)=0(m)/(s)`

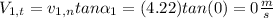
Equivalent head in centimetre of water column:

`H_(water)=H((rho_(air))/(rho_(water)))\\\\H_(water)=((w)/(g) )(r_(2)V_(2,t)-r_(1)V_(1,t))((rho_(air))/(rho_(water))) \\\\H_(water)=((78.54)/(9.81))((0.24)(1.643)-(0.12)(0)})((1.2)/(998))=38m=380cm`

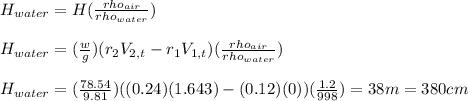
Break horse power:

`bhp=rho_(water) gHV=rho_(water) g[((w)/(g))(r_(2)V_(2,t)-r_(1)V_(1,t))]V\\\\bhp=(998)(9.81)[((78.54)/(9.81))((0.24)(1.643)-(0.12)(0))](0.573)=17710W=17.710kW`