Answer:
(12.1409, 14.0591
Explanation:
Given that Tensile strength tests were performed on two different grades of aluminum spars used in manufacturing the wing of a commercial transport aircraft. From past experience with the spar manufacturing process and the testing procedure, the standard deviations of tensile strengths are assumed to be known.
Group Group One Group Two
Mean 87.600 74.500
SD 1.000 1.500
SEM 0.316 0.433
N 10 12
The mean of Group One minus Group Two equals 13.100
standard error of difference = 0.556
90% confidence interval of this difference:
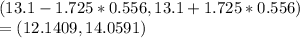
t = 23.5520
df = 20