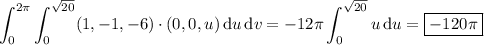Stokes' theorem allows for any choice of
 with
with
 as its boundary. The simplest region would be the disk
as its boundary. The simplest region would be the disk
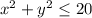 in the plane
in the plane
 , which can be parameterized using polar coordinates by
, which can be parameterized using polar coordinates by
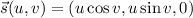
with
 and
and
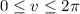 . Take the normal vector to
. Take the normal vector to
 to be
to be
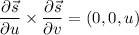
Then by Stokes' theorem,
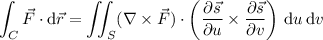
where
 denotes the curl of
denotes the curl of
 . The curl is
. The curl is

so the line integral has a value of