Question

on a hot summer day 609 people used the public pool the daily price for children is 1.50 and 2.00 for adults at the end of the day the receipt for admission totaled 1061.50 how many adult and how many children were at the pool that day

Answer 1

The number of children at the pool that day is 313

The number of adults at the pool that day is 296

Explanation:

Given as :

The Total number of people were using public pool = 609

The Total admission receipt collected at the day end = $1061.50

The entry price for children = $1.50

The entry price for adults = $2.00

Let The total number of children in the pool = c

And The total number of adults in the pool = a

Now, According to question

The Total number of people were using public pool = The total number of children in the pool + The total number of adults in the pool

or, c + a = 609 ...........1

And

The Total admission receipt collected at the day end = The entry price for children × The total number of children in the pool + The entry price for adults × The total number of adults in the pool

or, $1.50 × c + $2.00 × a = $1061.50

I.e 1.50 c + 2 a = 1061.50 ............2

Now, Solving equation 1 and 2

2 × (c + a) - (1.50 c + 2 a) = 2 × 609 - 1061.50

Or, 2 c + 2 a - 1.50 c - 2 a = 1218 - 1061.50

Or, (2 c - 1.50 c) + (2 a - 2 a) = 156.5

Or, 0.5 c + 0 = 156.5

∴ c =
`(156.5)/(0.5)`

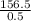
I.e c = 313

So, The number of children at the pool = c = 313

Now,

Put The value of c in eq 1

I.e ,c + a = 609

Or, 313 + a = 609

Or, a = 609 - 313

∴ a = 296

So, The number of adults at the pool = a = 296

Hence The number of children at the pool that day is 313

And The number of adults at the pool that day is 296 Answer