Question

A 1000 gallon tank, initially full of water, develops a leak at the bottom. Given that 300 gallons of water leak out in the first 30 minutes, find the amount of water, A(t), left in the tank t minutes after the leak develops if the water drains off at a rate proportional to the amount of water present.

a. A(t)= 1000(1/3)^1/10t
b. A(t)= 1000(1/2)^-1/10t
c. A(t)= 1000(1001/2)^t
d. A(t)= 1000e ^-1/10t
e. A(t)= 1000(1/2)^1/10t
f. None of these

Answer 1

option F

Explanation:

given,

capacity of tank = 1000 gallon

volume of water leak = 300 gallon

time = 30 min

water is leaking at the rate

formula used

`A = B e^(-kt)`

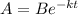
At t = 0 A = 1000 gallons

`1000= B e^(-k* 0)`

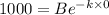
B = 1000

`A = 1000 e^(-kt)`

at t = 30 A = 700

`700= 1000 e^(-k* 30)`

`e^(-k* 30)=0.7`

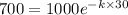
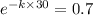
taking ln both side

`-k* 30=ln(0.7)`

`k=-(ln(0.7))/(30)`

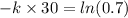
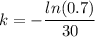
now,

`A = 1000 e^{(ln(0.7))/(30)t}`

`A = 1000* 0.7 e^{(t)/(30)}`

`A = 700 e^{(t)/(30)}`

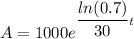
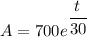
hence, the correct answer is option F