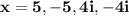Answer:
x = 5, -5, 4i, -4i ;
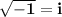
Explanation:
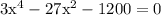
assume
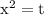

Now the above equation is a quadratic equation.
There are two solutions of any quadratic equation. Solution of a quadratic equation
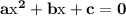 is given by:
is given by:
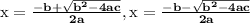
similarly there are two solutions of the quadratic equation
 which are:
which are:
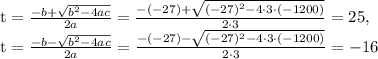
Since
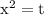
Therefore
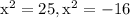
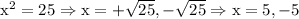
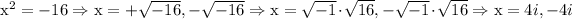 ; where
; where
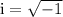 (the numbers with 'i' are called imaginary numbers)
(the numbers with 'i' are called imaginary numbers)
Therefore