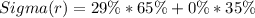Question

You manage a risky portfolio with an expected rate of return of 17% and a standard deviation of 29%. The T-bill rate is 8%. Your client chooses to invest 65% of a portfolio in your fund and 35% in an essentially risk-free money market fund. What is the expected return and standard deviation of the rate of return on his portfolio? (Do not round intermediate calculations. Round "Standard deviation" to 1 decimal place.)

Answer 1

13.85% and 18.9%

Step-by-step explanation:

As in this exercise we have a free risk asset we will assume that the t-bill has a standard deviation of 0%, so let´s firts calculate the expected return:

`E(r)=r_(1)*w_(1) +r_(2)*w_(2) +....+r_(n)*w_(n)`

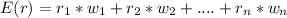
where E(r) is the expected return,
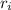`r_(i)` is the return of the i asset and
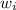`w_(i)` is the investment in i asset, so applying to this particular case we have:

`E(r)=17\%*65\%+8\%*35\%`

`E(r)=13.85\%`

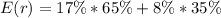
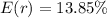
the calculation of standar deviation follows the same logic of the previous formula:

`Sigma(r)=29\%*65\%+0\%*35\%`

`Sigma(r)=18.9\%`