Question

Whats the equation of the line that passes threw -4,4 and is parrell to the line y=1/2-4

Answer 1

`y=(1)/(2)x+6`

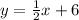
Explanation:

Given:

The equation of the known line is:

`y=(1)/(2)x-4`

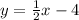
A point on the unknown line is (-4, 4)

Now, since the two lines are parallel, their slopes must be equal.

Now, slope of the known line is the coefficient of 'x' which is
`(1)/(2)`.

Therefore, the slope of the unknown line is also
`m=(1)/(2)`

Now, for a line with slope 'm' and a point on it
`(x_1,y_1)` is given as:

`y-y_1=m(x-x_1)`

Here,
`m=(1)/(2), x_1=-4,y_1=4`. Therefore,

`y-4=(1)/(2)(x-(-4))\\\\y-4=(1)/(2)(x+4)\\\\y-4=(1)/(2)x+2\\\\y=(1)/(2)x+2+4\\\\y=(1)/(2)x+6`

Hence, the equation of the unknown line is
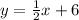`y=(1)/(2)x+6`.