Question

A certain type of flashlight requires two type-D batteries, and the flashlight will work only if both its batteries have acceptable voltages. Suppose that 90% of all batteries from a certain supplier have acceptable voltages. Among twenty randomly selected flashlights, what is the probability that at least nineteen will work? (Round your answer to three decimal places.) What assumptions did you make in the course of answering the question posed?

Answer 1

The probability that at least nineteen flashlight will work is 0.084.

The assumptions made are:

- The probability of the batteries having acceptable voltages are independent.

- The probability of the flashlight working depends only in the acceptable voltage of the batteries.

Explanation:

For the flashlight to operate, the two batteries have to have acceptable voltage. The probability of this event (flashlight working correctly) is the product of the probability of two batteries having acceptable voltages:

`P(w)=P(v)\cdot P(v)=0.9*0.9=0.81`

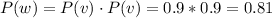
To answer what is the probability that at least nineteen flashlights will work out of a sample of twenty, we can model as a binomial variable (parameters n=20 and p=0.81).

The probability of at least 19 working is the sum of the probability of 19 and 20 flashligths working:

`P(k)=(n!)/(k!(n-k)!) p^k(1-p)^(n-k)\\\\P(19)=(20!)/(19!1!) *0.81^(19)*0.19^1=20*0.018*0.19=0.069\\\\P(19)=(20!)/(20!0!) *0.81^(20)*0.19^0=1*0.015*1=0.015\\\\P(X>19)=P(19)+P(20)=0.069+0.015=0.084`

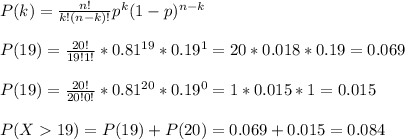
The assumptions made are:

- The probability of the batteries having acceptable voltages are independent.

- The probability of the flashlight working depends only in the acceptable voltage of the batteries.