Answer:
The wavelength of light is 2772 μm.
Step-by-step explanation:
Given that,
Frequency = 1580 cm⁻¹
Higher state =5
Lower state = 2
We need to calculate the energy for n = 5
Using formula of energy

Put the value into the formula
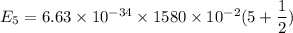
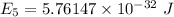
For n = 2,
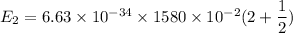

We need to calculate the energy
Using formula of energy
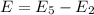
Put the value into the formula


We need to calculate the wavelength
Using formula of wavelength
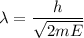
Put the value into the formula
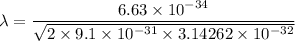
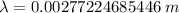
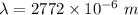
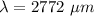
Hence, The wavelength of light is 2772 μm.