Question

A park ranger is looking out from their station at a 30 degree angle of depression. The ranger is 80 feet above the ground. How far is it from the ranger up in the station down to the fire?

Answer 1

Distance from the ranger up in the tower to the fire on the ground is 160 feet

Solution:

Given that park ranger is looking out from their station at a 30 degree angle of depression

The ranger is 80 feet above the ground

To find: Distance from the ranger up in the tower to the fire on the ground

The diagram is attached below

Consider a right angled triangle ABC

AB is the height of ranger above ground

The distance from the ranger up in the tower to the fire on the ground is the hypotenuse AC of the right triangle ABC.

The angle of depression from the ranger at point A and the angle of elevation from the fire on the ground at Point C are congruent (interior opposite angles).

Therefor, angle c = 30 degrees

Length of AB = 80 feet

We know that,

`sin \theta = (opposite)/(hypotenuse)\\\\sin \theta = (AB)/(AC)`

`sin 30 = (80)/(AC)\\\\(1)/(2) = (80)/(AC)\\\\AC = 80 * 2 = 160`

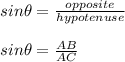
Thus the distance from the ranger up in the tower to the fire on the ground is 160 feet