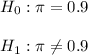Question

Test the claim that the proportion of people who own cats is significantly different than 90% at the 0.1 significance level.

The null and alternative hypothesis would be:

A. H0:p≥0.9H0:p≥0.9
H1:p<0.9H1:p<0.9

B. H0:p=0.9H0:p=0.9
H1:p≠0.9H1:p≠0.9

C. H0:p≤0.9H0:p≤0.9
H1:p>0.9H1:p>0.9

D. H0:μ=0.9H0:μ=0.9
H1:μ≠0.9H1:μ≠0.9

E. H0:μ≤0.9H0:μ≤0.9
H1:μ>0.9H1:μ>0.9

F. H0:μ≥0.9H0:μ≥0.9
H1:μ<0.9H1:μ<0.9

The test is:A. left-tailedB. two-tailedC. right-tailed

Answer 1

The right answer is Option B:

`H_0: \pi=0.9\\\\H_1: \pi\\eq0.9`

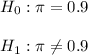
Explanation:

In this case we have to perform a hypothesis test on the proportion of the people owning cats.

The claim is that the proportion is significantly different than 905, what means it can be greater or smaller than 90% to reject the null hypothesis. Because of that, the null hypothesis has to state an equality (H0:p=0.9).

The right answer is Option B:

`H_0: \pi=0.9\\\\H_1: \pi\\eq0.9`