Answer:
Charles Second jump was
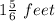 long.
long.
Explanation:
Given:
First Jump marked distance =

 can be Rewritten as
can be Rewritten as
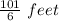
First Jump distance =
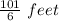
Second Jump marked distance =
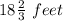
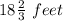 can be Rewritten as
can be Rewritten as
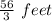
Second Jump distance =
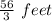
We need to find the how much long is Charles second jump.
To find Length of Second Jump is calculated by subtracting distance of First Jump from Distance of Second jump.
Length of Second Jump = Second Jump distance - First Jump distance
Substituting the values we get.
Length of Second Jump =

We will make denominator common by taking LCM and then solve for it.
Length of Second Jump =
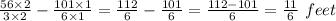
Now
 can be Rewritten as
can be Rewritten as
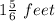
Length of Second Jump =
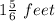
Hence Charles Second jump was
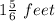 long.
long.