Question

To the nearest unit, what is the perimeter of this pentagon?

5
4
3
2
1
65
-3 -2 -1
2 3
4
بي ط ا
27 units
29 units
30 units
34 units

Answer 1

The perimeter of the pentagon is;

29 units

Explanation:

Let A, B, C, D, and E represent the vertices of the pentagon

The "x" and "y" coordinates of the vertices of the pentagon are given as follows;

A(-6, 2), B(-2, -2), C(5, -2), D(5, 2), E(-2, 5)

The length of the sides between each pair of coordinates can be found using the following formula;

`l = \sqrt{\left (y_(2)-y_(1) \right )^(2)+\left (x_(2)-x_(1) \right )^(2)}`

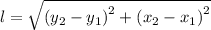
Therefore, we have;

Length of segment AB = √((-2 - (2))² + (-2 - (-6))²) = 4·√2

Length of segment BC = √((-2 - (-2))² + (5 - (-2))²) = 7

Length of segment CD = √((5 - 5)² + (2 - (-2))²) = 4

Length of segment DE = √((5 - 2)² + (-2 - 5)²) = √58

Length of segment EA = √((5 - (2))² + (-2 - (-6))²) = 5

The length of the perimeter of the pentagon = 5+√58 + 4 + 7 + 4·√2 ≈ 29.2726273554 ≈ 29

The length of the perimeter of the pentagon ≈ 29.