Question

A credit card company receives numerous phone calls throughout the day from customers reporting fraud and billing disputes. Most of these callers are put "on hold" until a company operator is free to help them. The company has determined that the length of time a caller is on hold is normally distributed with a mean of 2.5 minutes and a standard deviation 0.5 minutes. If 1.5% of the callers are put on hold for longer than x minutes, what is the value of x?

Answer 1

The value of X is 3.6 minutes.

Explanation:

We assume that the time on hold follows a normal distribution with

`\mu=2.5\\\\ \sigma=0.5`

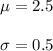
To calculate how many minutes the 1.5% of the customers are put on hold, we have to determine the z-value for this probability (P=0.015).

Looking in a z-table, the z value is 2.17:

`P(z>2.17)=0.015`

This can be translated to our distribution as:

`X=\mu+z*\sigma=2.5+2.17*0.5=2.5+1.085\approx3.6`

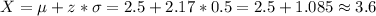
The value of X is 3.6 minutes.