Height of another tree that cast a shadow which is 20ft long is 5 feet approximately
Solution:
Given that tree with a height of 4 ft casts a shadow 15ft long on the ground
Another tree that cast a shadow which is 20ft long
To find: height of another tree
We can solve this by setting up a ratio comparing the height of the tree to the height of the another tree and shadow of the tree to the shadow of the another tree

Let us assume,
Height of tree =

Length of shadow of tree =
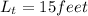
Height of another tree =
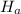
Length of shadow of another tree =
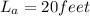
Set up a proportion comparing the height of each object to the length of the shadow,
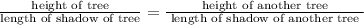
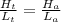
Substituting the values we get,

So the height of another tree is 5 feet approximately