Question

Charges of -q and 2q are fixed in place, with a distance of 2 m between them. A dashed line is drawn through the negative charge, perpendicular to the line between the charges. On the dashed line, at a distance L from the negative charge, there is at least one spot where the total potential is zero. Find L.

Answer 1

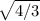`√(4/3)` = 1.155 m

Step-by-step explanation:

To solve for this question, we need to put a dummy charge at the location of distance L given. Lets say we put a charge +q at that position.

The distance of +q from -q is L

The distance of +q from 2q is sqrt(L^2 + 2^2) (Note that the three charges form a right angle triangle lines, so we use Phytagorean Theorem)

To have zero total potential, we need the sum of electric potential acting on the charge equal to zero.

Since -q is negative charge, it will attract +q

Since 2q is positive charges, it will repel +q

So, to have 0 electric potential,

total attraction from -q + total repulsion from 2q = 0

Uq1 + Uq2 = 0

Uq2 = -Uq1

Electric potential Energy for -q:

Uq1 = k(+q)(-q)/L = -k(q^2)/L

Electric potential energy for 2q:

Uq2 = k(q)(2q)/sqrt(L^2+2^2)

Applied both potential energy into total energy formula we get

Uq2 = -Uq1

k(q)(2q)/sqrt(L^2+2^2) = k(q^2)/L

2(q^2)k/sqrt(L^2 + 4) = (q^2)k/L

2/sqrt(L^2 + 4) = 1/L

2L = sqrt(L^2+4)

4L^2 = L^2 + 4

3L^2 = 4

L^2 = 4/3

L = sqrt(4/3) = 1.155 m