Question

Five hundred randomly selected automobile owners were questioned on the main reason they had purchased their current automobile. The results are given below.

STYLING ENGINEERING FUEL ECONOMY TOTAL
MALE 70 130 150 350
FEMALE 30 20 100 150
TOTAL 100 150 250 500

Give your conclusion for this test with 90% confidence level.

Answer 1

`\chi^2 =31.746`

`p_v =P(\chi^2_(2)>31.746)=1.2x10^(-7)`

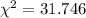
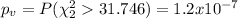
Since our calculated value it's higher than the critical value we have enough evidence to reject the null hypothesis of independence, and there would be a dependence between the gender and the type of automobile.

Explanation:

Previous concepts

The Chi-Square test of independence is used "to determine if there is a significant relationship between two nominal (categorical) variables". And is defined with the following statistic:

`\chi^2 =\sum_(i=1)^n ((O-E)^2)/(E)`

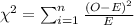
Where O represent the observed values and E the expected values.

State the null and alternative hypothesis

Null hypothesis: Styling engineering and fuel economy are independent

Alternative hypothesis: Styling engineering and fuel economy are dependent

The observed values are given by the table given:

STYLING ENGINEERING FUEL ECONOMY TOTAL

MALE 70 130 150 350

FEMALE 30 20 100 150

TOTAL 100 150 250 500

Calculate the expected values

In order to calculate the expected values we can use the following formula for each cell of the table:

`E = (row total* Column total)/(Grand total)`

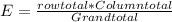
The following tables represent the xpected values calulated:

STYLING ENGINEERING FUEL ECONOMY TOTAL

MALE 70 105 175 350

FEMALE 30 45 75 150

TOTAL 100 150 250 500

Calculate the statistic

`\chi^2 =((70-70)^2)/(70)+((130-105)^2)/(105)+((150-175)^2)/(175)+((30-30)^2)/(30)+((20-45)^2)/(45)+((100-75)^2)/(75)`

`\chi^2 =31.746`

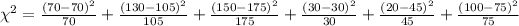
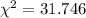
Calculate the critical value

First we need to calculate the degrees of freedom given by:

`df= (rows-1)(columns-1)=(2-1)(3-1)= 2`

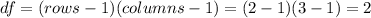
Since the confidence provided is 90% the significance would be
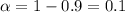`\alpha=1-0.9=0.1` and we can find the critical value with the following excel code: "=CHISQ.INV(0.9,2)", and our critical value would be
`\chi^2_(crit)=4.650`

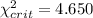
We can calculate also the p value:

`p_v =P(\chi^2_(2)>31.746)=1.2x10^(-7)`

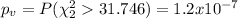
And we got the same decision reject the null hypothesis at 10% of significance.

Conclusion

Since our calculated value it's higher than the critical value we have enough evidence to reject the null hypothesis of independence, and there would be a dependence between the gender and the type of automobile.