Question

Find the area under one arch of the cycloid x = r(θ − sin(θ)) y = r(1 − cos(θ)).

Answer 1

`A_(c) =3\pi r^(2)`

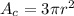
Explanation:

We can define the area under arch of the cycloid as:

`A_(c) = \int_(a)^(b) ydx`

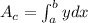
Let's evaluate this integral between 0 and 2π and put it in terms of dθ, using the chain rule.

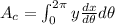`A_(c) = \int_(0)^(2\pi) y(dx)/(d\theta)d\theta` (1)

Taking the derivative of x we have:

`(dx)/(d\theta) = r(1 - cos(\theta))` (2)

Now, we can put (2) in (1).

`A_(c)=\int_(0)^(2\pi) r(1 - cos(\theta))\cdot r(1 - cos(\theta))d\theta = \int_(0)^(2\pi) r^(2)(1 - cos(\theta))^(2)d\theta`

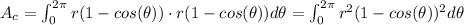
We can solve the quadratic equation to solve this integral:

`A_(c) = \int_(0)^(2\pi) r^(2)(1 - cos(\theta))^(2)d\theta=r^(2)\int_(0)^(2\pi) (1-2cos(\theta)+cos^(2)(\theta))d\theta`

Now, we just need to take this integral by the sum rule. Let's recall we can use integration by part to solve cos²(θ)dθ.

`A_(c) = r^(2)(\theta |_(0)^(2\pi) - 2sin(\theta)|_(0)^(2\pi) + 0.5\theta|_(0)^(2\pi) - 0.25sin(2\theta)|_(0)^(2\pi))`

Finally, the area is:

`A_(c) = r^(2)(2\pi + \pi)=3\pi r^(2)`

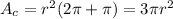
Have a nice day!