Question

Midpoint (23,- 10), endpoint (15.-16)
The other endpoint is

Answer 1

The other endpoint is (31, -4)

Solution:

Given that midpoint (23,- 10), endpoint (15.-16)

To find: The other endpoint

The formula for midpoint is given as:

`\text {For two points }\left(x_(1), y_(1)\right) \text { and }\left(x_(2), y_(2)\right), \text { the midpoint }(x, y) \text { is given as: }`

`m(x, y)=\left((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2)\right)`

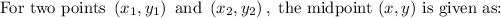
Here in this problem,

`m(x, y) = (23, -10)`

`(x_1, y_1) = (15, -16)`

`(x_2, y_2) = ?`

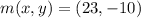
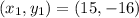
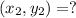
Substituting the values in formula we get,

`(23,-10)=\left((15+x_(2))/(2), (-16+y_(2))/(2)\right)`

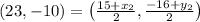
On comparing both sides we get,

`23=(15+x_(2))/(2) \text { and }-10=(-16+y_(2))/(2)`

`\begin{array}{l}{46=15+x_(2) \text { and }-20=-16+y_(2)} \\\\ {x_(2)=46-15 \text { and } y_(2)=-20+16} \\\\ {x_(2)=31 \text { and } y_(2)=-4}\end{array}`

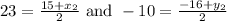
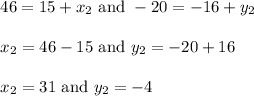
Thus the other endpoint is (31, - 4)