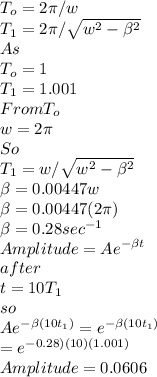This Question has mistakes.Correct question is
An undamped oscillator has period τo=1.000s , but I now add a little damping so that its period changes to τ1=1.001s.
What is the damping factor β? By what factor will the amplitude of oscillation decrease after 10 cycles? Which effect of damping would be more noticeable, the change of period or the decrease of the amplitude?
Answer:
β=0.28 /sec
Amplitude=0.0606
Step-by-step explanation: