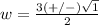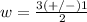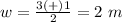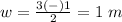Question

una ventana rectangular tiene l metros de ancho y h metros de altura, con un perímetro de 6 metros y un área de 2m² ¿cuál es la fórmula para calcular el ancho de la ventana?​

Answer 1

The formula for calculating the width of the window is

`w=\frac{-(-3)(+/-)\sqrt{-3^(2)-4(1)(2)}} {2(1)}`

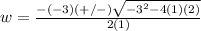
Explanation:

The question in English is

A rectangular window is l meters wide and h meters high, with a perimeter of 6 meters and an area of 2m². What is the formula for calculating the width of the window?

we know that

The perimeter of the window is equal to

`P=2(l+w)`

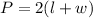
we have

`P=6\ m`

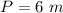
so

`6=2(l+w)`

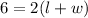
simplify

`3=(l+w)`

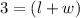
isolate the variable l

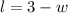`l=3-w` ----> equation A

The area of the window is equal to

`A=lw`

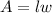
we have

`A=2\ m^2`

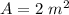
so

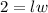`2=lw` ----> equation B

substitute equation A in equation B

`2=(3-w)w`

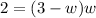
solve for w

`2=3w-w^2`

`w^2-3w+2=0`

The formula to solve a quadratic equation of the form

`ax^(2) +bx+c=0`

is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`w^2-3w+2=0`

so

`a=1\\b=-3\\c=2`

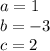
substitute in the formula

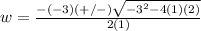`w=\frac{-(-3)(+/-)\sqrt{-3^(2)-4(1)(2)}} {2(1)}` ---> formula for calculating the width of the window

`w=\frac{3(+/-)√(1)} {2}`

`w=\frac{3(+/-)1} {2}`

`w=\frac{3(+)1} {2}=2\ m`

`w=\frac{3(-)1} {2}=1\ m`