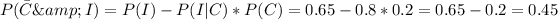Question

According to Reuters, a survey undertaken by the National Center for Health Statistics revealed that about 25% of U.S. households have only a cell phone (no land line). According to the FCC, 65% of U.S. households have high-speed Internet. Suppose of U.S. households having only a cell phone, 80% have high-speed Internet. A U.S. household is randomly selected.

a. What is the probability that the household has only a cell phone and has high-speed Internet?
b. What is the probability that the household has only a cell phone or has high-speed Internet?
c. What is the probability that the household has only a cell phone and does not have high-speed Internet?
d. What is the probability that the household does not have just a cell phone and does not have high-speed Internet?
e. What is the probability that the household does not have just a cell phone and does have high-speed Internet?

Answer 1

a) P=0.8

b) P=0.67

c) P=0.05

d) P=0.33

e) P=0.45

Explanation:

a. What is the probability that the household has only a cell phone and has high-speed Internet?

This probability is stated in the question: "Suppose of U.S. households having only a cell phone, 80% have high-speed Internet", so the probability is P=0.8.

`P(C\&I)=0.8`

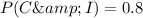
b. What is the probability that the household has only a cell phone or has high-speed Internet?

This probability is equal to the sum of the probability of having only a cell phone and the probability of having high-speed internet, less the probability of having both (to avoid counting this household twice).

`P(C\,orI\,)=P(C)+P(I)-P(C)*P(I|C)=0.25+0.65-(0.25*0.8)=0.25+0.62-0.20=0.67`

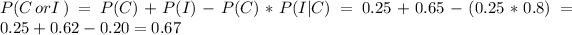
c. What is the probability that the household has only a cell phone and does not have high-speed Internet?

This is equal to the probability of not having high-speed internet given that it has a cell phone (complementaty of the proability of Point (a)) multiplied by the probability of having a cell phone.

`P(C\&\bar I)=P(\bar I|C)*P(C)=(1-P(\I|C))*P(C)=(1-0.8)*0.25 = 0.2*0.25 = 0.05`

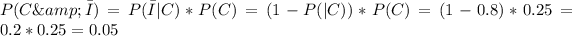
d. What is the probability that the household does not have just a cell phone and does not have high-speed Internet?

This probability is complementary of the one calculated in Point (c).

`P(\bar C \,or\, \bar I)=1-P(C\, or\,I)=1-0.67=0.33`

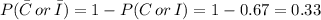
e. What is the probability that the household does not have just a cell phone and does have high-speed Internet?

This is equal to the probability of having high-speed internet less the probability it has both (cell phone and internet).

`P(\bar C\&I)=P(I)-P(I|C)*P(C)=0.65-0.8*0.2=0.65-0.2=0.45`