Answer:
The minimum sample size required is 5,499 computer users.
The major obstacle is that it is a big sample size if it is a small organization wanting to perform it.
Explanation:
We need to calculate a sample size in order to have 95% confidence interval with 12 minutes of witdth.
So, we have that the difference between the upper limit and the lower limit is 12:
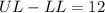

For a 95% CI, the value of z is 1.96. The standard deviation is 227.
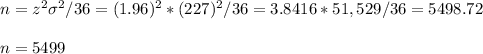
The minimum sample size required is 5,499 computer users.